Олимпиадная задача: равенство диагоналей в выпуклом семиугольнике. Планиметрия 8–9 класс
Задача
В выпуклом семиугольнике A1A2A3A4A5A6A7 диагонали A1A3, A2A4, A3A5, A4A6, A5A7, A6A1 и A7A2 равны между собой. Диагонали A1A4, A2A5, A3A6, A4A7, A5A1, A6A2 и A7A3 тоже равны между собой. Обязательно ли этот семиугольник равносторонний?
Решение
Решение 1:Равнобедренные трегольники A1A3A5 и A3A5A7 равны по трём сторонам. Поэтому ∠A3A1A5 = ∠A3A7A5, то есть точки A1, A3, A5 и A7 лежат на одной окружности. Аналогично на одной окружности лежат точки A3, A5, A7 и A2. Однако это – та же окружность. Так продолжая, получаем, что все вершины лежат на этой окружности. Ясно, что они делят её на семь равных дуг (например, ⌣A1A2 = ⌣A1A4 – ⌣A2A4 = ⌣A2A5 – ⌣A3A5 = ⌣A2A3). Таким образом, семиугольник не только равносторонний, но и правильный.
Решение 2:Равны все равнобедренные трегольники вида AiAi+2Ai+4 (см. рис.; мы считаем A8 = A1, A9 = A2 и т.д.). Поэтому равны все углы вида AiAi+3Ai+1 (как разности углов Ai+1Ai+3Ai+5 и AiAi+3Ai+5). Значит, равны и все трегольники AiAi+3Ai+1 (по двум сторонам и углу между ними), и, следовательно, равны и все отрезки AiAi+1.
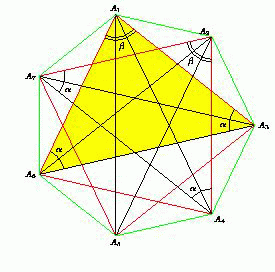
Ответ
Обязательно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь