Олимпиадная задача по планиметрии для 8 и 9 класса: сумма углов внутри квадрата
Задача
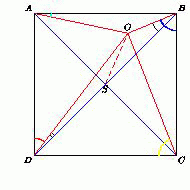
Дан квадрат, внутри которого лежит точка O. Докажите, что сумма углов OAB, OBC, OCD и ODA отличается от 180° не больше чем на 45°.
Решение
Пусть S – центр квадрата. Можно считать, что точка O принадлежит треугольнику ASB. Поскольку в треугольнике OBD OD ≥ OB, то ∠OBD ≥ ∠BDO, и поэтому ∠OBC + ∠ODA = 45° + 45° + (∠OBD – ∠BDO) ≥ 90°. Кроме того, ∠OCD ≥ ∠ACD = 45°, значит, рассматриваемая сумма больше
90° + 45° = 135° = 180° – 45°.
По тем же причинам сумма ∠OAD + ∠ODC + ∠OCB + ∠OBA больше 180° – 45°. Наша сумма дополняет её до 360°, то есть она меньше 180° + 45°.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет