Назад

Олимпиадная задача по планиметрии для 8-9 классов: равнобедренный треугольник и медианы

Задача 208210 • Сложность: 3 • 8-9 класс
Задача

В треугольнике ABC медианы AA' , BB' и CC' продлили до пересечения с описанной окружностью в точках A0, B0и C0соответственно. Известно, что точка M пересечения медиан треугольника ABC делит отрезок AA0пополам. Докажите, что треугольник A0B0C0– равнобедренный.

Решение

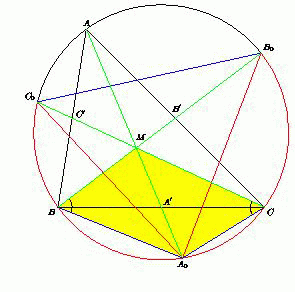Медианы треугольника делятся их точкой пересечения в отношении 2:1, считая от вершины треугольника, поэтому, если MA'=x , то AM=2x . По условию задачи MA0 = AM = 2x , поэтому

A'A0=MA0-MA' = 2x-x=x.

Значит, A' – середина отрезка MA0. Диагонали четырёхугольника BMCA0делятся точкой пересечения A' пополам, поэтому BMCA0– параллелограмм. Его противоположные углы MCA0и MBA0равны. Тогда равны вписанные углы A0CC0и A0BB0. Первый из них опирается на дугу A0BC0, а второй – на дугу A0CB0. Значит, эти дуги равны. Но тогда равны и стягивющие их хорды A0C0и A0B0. Следовательно, треугольник A0B0C0– равнобедренный.

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет