Назад

Олимпиадная задача по планиметрии для 8-9 класса от Емельянова Л. А.

Задача 208212 • Сложность: 3 • 8-9 класс
Задача

Три окружности ω1, ω2 и ω3 радиуса r проходят через точку S и касаются внутренним образом окружности ω радиуса R  (R > r)  в точках T1, T2 и T3 соответственно. Докажите, что прямая T1T2 проходит через вторую (отличную от S) точку пересечения окружностей ω1 и ω2.

Решение

  Обозначим через O1, O2, O3 и O центры окружностей ω1, ω2, ω3 и ω соответственно. Поскольку линия центров двух касающихся окружностей проходит через их точку касания, то точки O, O1 и T1 лежат на одной прямой, причём  OO1 = OT1 – O1T1 = R – r.

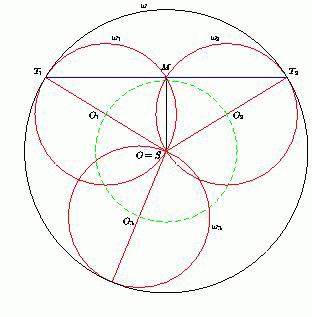
  Аналогично  OO2 = OO3 = R – r,  поэтому O – центр описанной окружности треугольника O1O2O3. Поскольку  SO1 = SO2 = SO3 = r,  точка S также является центром описанной окружности треугольника O1O2O3. Следовательно, точки S и O совпадают.

  Пусть M – точка пересечения ω1 и ω2. Поскольку T1O – диаметр ω1,  ∠OMT1 = 90°.  Аналогично,  ∠OMT2 = 90°.  Следовательно, точка M лежит на прямой T1T2.

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет