Олимпиадная задача по планиметрии для 8–9 классов: сумма площадей в квадратах

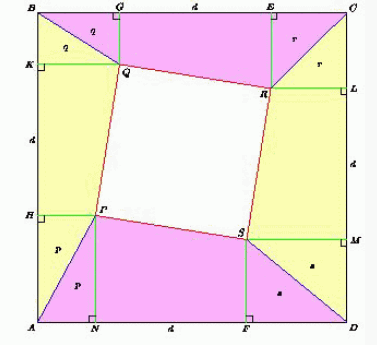  Пусть точки H и K – проекции точек P и Q на сторону AB квадрата ABCD, G и E – проекции точек Q и R на сторону BC, L и M – проекции точек R и S на сторону DC, F и N – проекции точек S и P на сторону AD. Предположим, что эти проекции расположены так, как показано на рисунке.   Поскольку последовательные стороны квадратов получаются друг из друга поворотом на угол 90°, то углы между прямыми AB и PQ, BC и QR, CD и RS, DA и SP равны. Поэтому равны и проекции HK, GE, LM и FN сторон меньшего квадрата на соответствующие стороны большего.

  Пусть сторона квадрата ABCD равна 1. Обозначим  HK = GE = LM = FN = d,  S_AHP = S_ANP = p,  S_BKQ = S_BGQ = q,  S_ECR = S_LRC = r,  S_MSD = S_FSD = s.

  Заметим, что  HP + MS = KQ + RL = 1 – d.  Тогда

S_APQB + S_CRSD = (S_AHP + S_BKQ + S_PHKQ) + (S_DMS + S_LRC + S_MSRL) = (p + q + ½ (PH + QK)d) + (r + s + ½ (RL + SM)d) =

= p + q + r + s + ½ ((PH + SM) + (QK + RL))d = p + q + r + s + (1 – d)d = p + q + r + s + (1 – d)d.

  Аналогично находим, что сумма площадей четырёхугольников APSD и BQRC также равна  p + q + r + s + (1 – d)d.  (Каждая из этих сумм равна  ½ (1 – d²).)

  Для любого другого расположения указанных точек через d обозначим величину проекции вектора 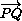   на направленную прямую AB. Такими же будут величины проекций  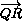  на BC,  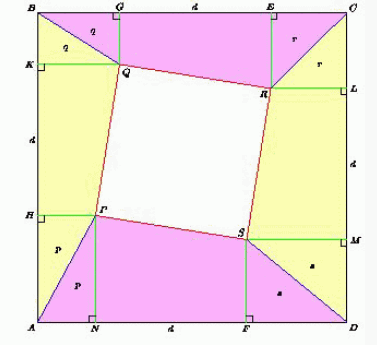  на CD и  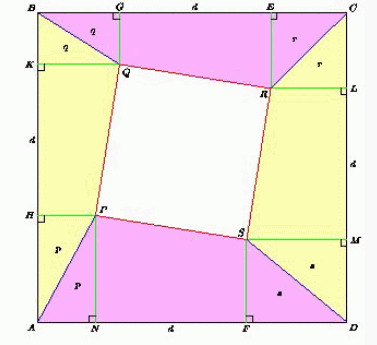  на DA. Чтобы получить площадь четырёхугольника APQB, нужно сумму  p + q  площадей треугольников APH и KQB увеличить (если  d > 0)  или уменьшить (если  d < 0)  на площадь трапеции KPQH. Остальное аналогично.

Ответ задачи отсутствует