Олимпиадная задача по планиметрии: равенство диагоналей в четырёхугольнике KLMN
Задача
KLMN – выпуклый четырёхугольник, в котором равны углы K и L. Серединные перпендикуляры к сторонам KN и LM пересекаются на стороне KL.
Докажите, что в этом четырёхугольнике равны диагонали.
Решение
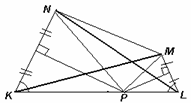
Так как точка P пересечения серединных перпендикуляров к отрезкам KN и LM равноудалена от концов каждого из этих отрезков, то треугольники KPN и LPM – равнобедренные (см. рис.). В этих треугольниках равны углы при основаниях, поэтому равны и углы при вершине Р.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет