Олимпиадная задача: нахождение суммы чисел в таблице без повторений строк и столбцов
Задача
Из таблицы
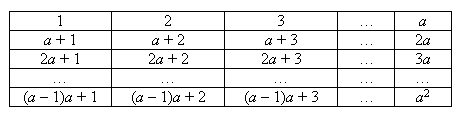
Решение
Представим нашу таблицу как сумму двух таблиц:

Ответ
½ a(a² + 1).
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет