Олимпиадная задача: площадь прямоугольника, вписанного в треугольник (8-9 класс)

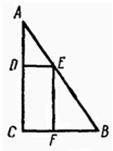
  Рассмотрим сначала случай, когда треугольник ABC прямоугольный и в него вписан прямоугольник DEFC так, что одна вершина прямоугольника совпадает с вершиной прямого угла треугольника, две другие вершины лежат на катетах и четвёртая – на гипотенузе (см. рис.). Обозначим  AC = b,

BC = a,  CD = EF = b₁,  DE = CF = a₁.  Из подобия треугольников ADE и ACB имеем  DA : AC = ED : BC,  или  (b – b₁) : b = a₁ : a,  откуда  b₁ = ^(a–a₁)b/_a.  Площадь прямоугольника равна  a₁b₁ = ^{a₁b(a–a₁)}/_a ≤ ^b/_a(^a/₂)² = ¼ ab = ½ S_ABC.

  В общем случае опустим из вершины B треугольникаABC, противоположной той, на которой лежат две вершины прямоугольника, высотуBH. Получим два прямоугольных треугольника, в которые вписаны прямоугольники, как и в предыдущем случае. Поэтому удвоенная площадь прямоугольника не превосходит  S_ABH + S_HBC = S_ABC.

Ответ задачи отсутствует