Олимпиадная задача: Сколько корней имеет уравнение sin x = x/100? Тригонометрия, 9–11 класс
Задача
Сколько корней имеет уравнение sin x=x/100?
Решение
Задачу легко решить на графике. Поскольку графики синуса и функции y=x/100симметричны относительно начала координат, то
достаточно рассмотреть правую часть графиков. Максимальное значение
синуса равно 1. Поэтому точки пересечения графиков будут находиться
в пределах тех значений x , для которых x/100не
превосходит 1, т. е. в пределах от 0 до 100. В этом промежутке
содержится100/2π периодов sin x ,100/2π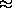 15,9. В каждом периоде для sin x синусоида и график прямой y=100/x имеют две точки
пересечения, причём в первой половине периода (рис.). Поэтому в
пределах 15,5 периодов будет содержаться 32 точки пересечения
графиков. Столько же точек пересечения графиков будет находиться
слева от начала координат, но при этом необходимо учесть, что начало
координат считается нами два раза. Поэтому всего данное уравнение
имеет 63 корня.
15,9. В каждом периоде для sin x синусоида и график прямой y=100/x имеют две точки
пересечения, причём в первой половине периода (рис.). Поэтому в
пределах 15,5 периодов будет содержаться 32 точки пересечения
графиков. Столько же точек пересечения графиков будет находиться
слева от начала координат, но при этом необходимо учесть, что начало
координат считается нами два раза. Поэтому всего данное уравнение
имеет 63 корня.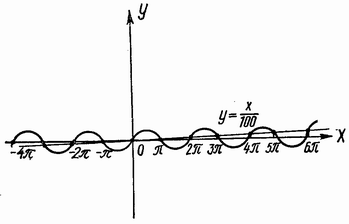
Ответ
63 корня.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь