Олимпиадная задача по алгебре для 10–11 классов: решение уравнения с синусом и степенями
Задача
Решите уравнение: (x³ – 2)(2sin x – 1) + (2x³ – 4) sin x = 0.
Решение
Из того, что функция y = 2t возрастает, следует:
1) если sin x > 0, то 2sin x – 1 > 0; если sin x < 0, то 2sin x – 1 < 0;
2) если x³ – 2 > 0, то 2x³ – 4 > 0; если x³ – 2 < 0, то 2x³ – 4 < 0.
Следовательно, если (x³ – 2)(2sin x – 1) > 0, то (2x³ – 4) sin x > 0; если (x³ – 2)(2sin x – 1) < 0, то (2x³ – 4) sin x < 0; то есть знаки выражений
(x³ – 2)(2sin x – 1) и (2x³ – 4) sin x совпадают. Поэтому, каждое слагаемое в левой части уравнения должно обращаться в нуль, то есть x³ = 2 или sin x = 0.
Ответ
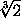 , πn (n ∈ Z).
, πn (n ∈ Z).
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет