Задание олимпиады: доказательство для выборов в городе N

Задача

У каждого из жителей города N знакомые составляют не менее 30 населения города. Житель идет на выборы, если баллотируется хотя бы один из его знакомых. Докажите, что можно так провести выборы мэра города N из двух кандидатов, что в них примет участие не менее половины жителей.

Решение

Решение Iосновано на следующей лемме.

Лемма. Пусть S – произвольное непустое множество жителей. Тогда в городе N найдется житель, знакомый не менее чем с30% жителей из S .

Обозначим через |X| количество жителей в множестве X . Оценим общее количество (упорядоченных) пар знакомых(t,s), где t – произвольный человек, а s – человек из S . Для каждого s₀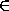 S количество пар вида(t,s₀)не меньше0,3|N| , поэтому общее количество пар не меньше0,3|S||N| . Поэтому для какого-то человека t₀ количество пар вида(t₀,s)не меньше0,3|S| , что и требовалось.

Выдвинем в качестве первого кандидата произвольного жителя A . Рассмотрим множество S не знакомых с A жителей. Если множество S пусто, то в качестве второго кандидата можно взять любого жителя города N , отличного от A . Если множество S непусто, то, применив лемму, найдем жителя B , знакомого не менее чем с 30 жителей, входящих в S . Покажем, что выборы из двух кандидатов A и B удовлетворяют решению задачи.

Пусть житель A имеет k знакомых, а общее число жителей в N равно n . Тогда на выборы из двух кандидатов A и B придет не менее k+0,3· (n-k)=0,3n+0,7k жителей, и так как k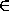0,3n , то в выборах примет участие не менее0,3n+0,7· 0,3n=0,51n , т.е. более половины жителей N . Решение IIОбозначим через n число жителей в городе N . Для любых двух жителей города подсчитаем число жителей, знакомых хотя бы с одним из них, и обозначим сумму всех полученных чисел через. Мы должны доказать, что в городе N найдутся два таких жителя A и B , что число жителей, знакомых или с A , или с B , не меньше0,5n . 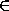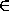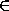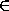Так как число пар жителей равно , то для этого достаточно показать, что 0,5n· =n .

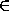
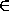
Для каждого жителя M оценим число(M)пар жителей, в которых хотя бы один человек знаком с M . Для этого оценим количество всех остальных пар: в каждой из них оба человека не знакомы с M , поэтому количество таких пар не превосходит 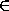; поскольку общее количество пар жителей равно 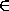, получаем, что(M)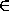 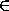> 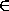, поэтому >n 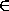, что и требовалось.