Олимпиадная задача: комитеты и депутаты – доказательство общих членов (8-10 класс)

Решение 1:   Обозначим  n = 16000.  Предположим, что каждые два комитета имеют не более трёх общих членов. Пусть двое секретарей A и B составляют списки всевозможных председателей на три заседания Думы. A считает, что любой депутат может быть председателем на каждом из этих заседаний, поэтому у него получилось 1600³ списков. B считает, что на каждом заседании могут председательствовать только члены одного (неважно какого именно) комитета, поэтому сначала он запросил соответствующие списки от каждого комитета и получил 80³n списков. После этого B выбросил из списков, поданных i-м комитетом, те тройки, которые уже вошли в списки одного из предыдущих  i – 1  комитетов. Так как каждые два комитета (а таких пар 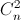 ) выдвинули всех своих общих членов, то B при формировании своих списков выбросил не более, чем  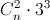  списков. Очевидно, что списков, которые составил A, не меньше, чем списков, которые составил B, то есть   1600³ ≥ 80³·n – ½ n(n – 1)·3³ > 80³·n – 16n² = (80³ – 16n)n = (2⁹·10³ – 2⁸·10³) = 1600³. Противоречие.

Решение 2:   Пусть всего имеется n комитетов, и n_i – число комитетов, куда входит i-й депутат. Выпишем для каждого депутата все пары комитетов, куда он входит. Всего будет выписано 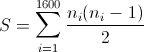    пар. По условию  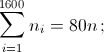   согласно неравенству между средним квадратичным и средним арифметическим     Поэтому  S ≥ 2n² – 40n.

  С другой стороны, если у каждой пары комитетов имеется не более трёх общих членов, то  S ≤ ³/₂ n(n – 1).  Отсюда  2n² – 40n ≤ ³/₂ n(n – 1),  то есть

4n – 80 ≤ 3n – 3.  Следовательно,  n ≤ 77.  Противоречие.

Ответ задачи отсутствует