Задание олимпиады: доказательство свойств окружностей и треугольника ABC, планиметрия

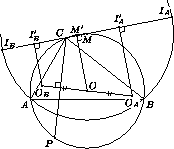
  Пусть M – середина отрезка I_AI_B . Поскольку биссектрисы внутреннего и внешнего углов перпендикулярны,  AI_A ⊥ AI_B  и  BI_A ⊥ BI_B. Значит, точки I_A и I_B лежат на окружности с диаметром AB, поэтому ∠AI_AB = ½ ∠AMB.  Заметим, что  ∠AI_AB = ½ (180° – ∠B) – ½ ∠A = ½ ∠C,  то есть  ∠AMB = ∠C.  Следовательно, точка M лежит на окружности Ω. Поскольку  AM = BM,  точка M является серединой дуги ACB этой окружности.

  Пусть I_A', I_B', M' – середины отрезков CI_A, CI_B, CM соответственно (см. рис.). Точки I_A', I_B', M' являются проекциями центров O_A, O_B, O описанных окружностей треугольников I_ACP, I_BCP, ABC на прямую I_AI_B. Точки O_A, O_B, O лежат на серединном перпендикуляре к отрезку CP. Поэтому достаточно доказать, что M' является серединой отрезка I_A'I_B'. Но это верно, поскольку M – середина I_AI_B, а тройка точек I_A', I_B', M' получается из тройки I_A, I_B, M гомотетией с центром C и коэффициентом ½.

Ответ задачи отсутствует