Олимпиадная задача по планиметрии для 8-10 класса от Емельянова Л. А.
Задача
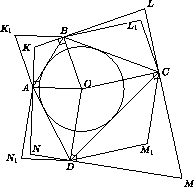
Четырехугольник ABCD описан около окружности. Биссектрисы внешних углов A и B пересекаются в точке K , внешних углов B и C – в точке L , внешних углов C и D – в точке M , внешних углов D и A – в точке N . Пусть K1 , L1 , M1 , N1 – точки пересечения высот треугольников ABK , BCL , CDM , DAN соответственно. Докажите, что четырехугольник K1L1M1N1 – параллелограмм.
Решение
Обозначим через O центр вписанной окружности четырехугольника ABCD . Поскольку внешняя и внутренняя биссектрисы угла
перпендикулярны, OA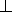 
NK , OB 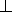KL .
Высота AK1 треугольника ABK перпендикулярна BK , поэтому AK1 || OB . Аналогично, BK1 || OA .
Следовательно, AOBK1 – параллелограмм, и точка K1 получается из точки A параллельным переносом на вектор 
= 
.
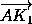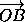Таким же образом, точка L1 получается из точки C параллельным переносом на вектор 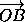. Поэтому 
=
.
=
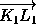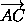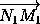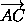, откуда следует, что K1L1M1N1 – параллелограмм.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь