Олимпиадная задача Берлова: доказательство алгебраического неравенства для n и x₁…xₙ, 8–10 класс
Задача
Даны натуральное число n > 3 и положительные числа x1, x2, ..., xn, произведение которых равно 1.
Докажите неравенство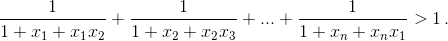 
Решение
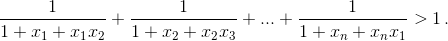
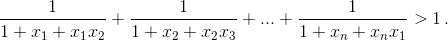Обозначим S = 1 + x1 + x1x2 + ... + x1x2...xn–1. Домножая числитель и знаменатель в втором слагаемом правой части на x1, в третьем – на x1x2, ..., в n-м – на x1x2...xn–1 и
учитывая, что x1x2...xn = 1, получаем
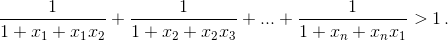
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет