Олимпиадная задача: траектория шара в правильном 1998-угольнике — планиметрия, Кожевников П. А.

  Обозначим траекторию шара B₁B₂...B₁₉₉₈B₁, где B₁ – середина A₁A₂. Также обозначим  α = ∠ B₂B₁A₂  (угол, под которым пустили шар),

φ = ∠B₁A₂B₂ = ^1996π/₁₉₉₈  – угол правильного 1998-угольника,  β = π – α – φ = ∠B₁B₂A₂ (см. рис.).

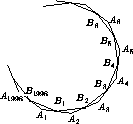
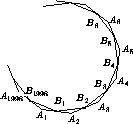  По закону отражения  ∠B₃B₂A₃= β.  Из треугольникаB₂A₃B₃ ∠B₂B₃A₃= π – β – φ = α,  снова по закону отражения  ∠B₄B₃A₄= α,  и т.д., наконец ∠B₁₉₉₈B₁A₁= α.  В результате получаем, что все треугольникиB₁A₂B₂,B₂A₃B₃, ...,B₁₉₉₈A₁B₁имеют углы α, β, φ и, следовательно, подобны друг другу. Пусть      – отношение соответствующих сторон в этих подобных треугольниках.   Имеем:  k·B₂A₂ = B₁A₂,  k·B₂A₃ = B₃A₃,  k·B₁₉₉₈A₁ = B₁A₁.  Сложив эти равенства, получим:  k(A₂A₃ + A₄A₅ + ... + A₁₉₉₈A₁) = A₁A₂ + A₃A₄ + ... + A₁₉₉₇A₁₉₉₈,  откуда  k = 1  в силу правильности многоугольника A₁A₂...A₁₉₉₈. Значит, все треугольники B₁A₂B₂, B₂A₃B₃, ..., B₁₉₉₈A₁B₁ – равнобедренные, и точки B₂, ..., B₁₉₉₈ – середины соответствующих сторон многоугольника A₁A₂...A₁₉₉₈. Это доказывает правильность многоугольника B₁B₂...B₁₉₉₈ (см. задачу 155719).

Ответ задачи отсутствует