Олимпиадная задача по тригонометрии: неравенство для остроугольного треугольника
Задача
При каких натуральных n для любых чисел α , β , γ , являющихся величинами углов остроугольного треугольника, справедливо неравенство
sin nα + sin nβ + sin nγ<0?
Решение
Для любого треугольника T с углами α , β , γ обозначим fn(T)= sin nα + sin nβ + sin nγ.
Лемма. Пусть x+y+z=π k , где k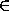
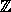. Тогда
| sin x|
| sin y|+| sin z|.
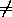π l , z 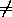π l , где l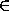 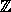, это неравенство – строгое.
| sin x|=| sin(y+z)|=| sin y cos z+ sin z cos y|
| sin y|· | cos z|+| sin z|· | cos y|| sin y|+| sin z|.
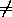π l , z 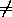π l , где l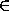 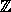, последнее неравенство строгое.
Излеммыследует, что знак функции fn(T)определяется двумя синусами, имеющими
одинаковые знаки: если, например, sin nα >0, sin nβ >0, то fn(T)
sin nα + sin nβ -| sin nγ|>0.
Очевидно, f1(T)>0. Для любого (не обязательно остроугольного) треугольника T справедливо и неравенство f2(T)>0.
В самом деле, если α <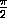
, β <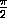 , то sin 2α >0, sin2β >0.
Пусть n=3. Рассмотрим равнобедренные остроугольные треугольники с углами α и β при основании: при изменении x=α =β от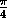 
до 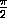величина3x меняется от 
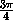до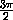 
. Следовательно, sin 3x (а вместе с ним и f(T)) принимает
как положительные, так и отрицательные значения.
Пусть n=4, α β γ . Поскольку треугольник остроугольный, β >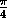 (если β 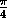, γ 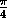, то α ).
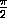Значит, π<4β 4α <4· 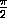=2π , откуда sin4α <0, sin4β <0. Вследствиелеммы f4(T)<0.
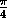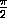Пусть n>4. Рассуждая как в случае n=3, получаем: при изменении x=α =β от до величина y=nx пробегает интервал,
длина которого больше π . Следовательно, найдутся точки x1 и x2 такие, что sin nx1>0, sin nx2<0.
Отсюда fn(T1)>0, fn(T2)<0, где T1 и T2 – треугольники, соответствующие x1 и x2.
Ответ
4.00
Чтобы оставлять комментарии, войдите или зарегистрируйтесь