Олимпиадная задача Берлова С. Л. о биссектрисах и сферах в треугольной пирамиде
Задача
Дана треугольная пирамида ABCD . Сфера S1 , проходящая через точки A , B , C , пересекает ребра AD , BD , CD в точках K , L , M соответственно; сфера S2 , проходящая через точки A , B , D , пересекает ребра AC , BC , DC в точках P , Q , M соответственно. Оказалось, что KL|| PQ . Докажите, что биссектрисы плоских углов KMQ и LMP совпадают.
Решение
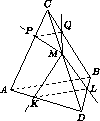
Тогда вписанные четырехугольники ABLK и ABQP являются трапециями, а,
значит, равнобокими трапециями. Поэтому 
DAB= DBA , CAB= CBA и треугольники ABD и ABC – равнобедренные.
Тогда пирамида ABCD симметрична относительно плоскости α – серединного перпендикуляра к AB , поскольку каждый из треугольников ABD и ABC симметричен относительно α . При этой симметрии точки K и L , а также P и Q переходят друг в друга, а точка M переходит в себя; поэтому углы KMQ и LMP переходят друг в друга.
Пусть β – плоскость, перпендикулярная к CD , проходящая через M ; поскольку C,D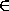
α , то β
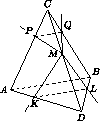α ; аналогично β CBD .
Поскольку четырехугольники BLMC и DMQB вписанные, имеем DML=180o- CML= CBD=180o- DMQ= CMQ .
Таким образом, лучи ML и MQ симметричны относительно β . Аналогично, MK и MP симметричны относительно β .
Отложим на лучах MK , ML , MP , MQ единичные отрезки MK' , ML' , MP' , MQ' . Тогда точки K' и L' , а также P' и Q' симметричны относительно α , а точки K' и P' , L' и Q' симметричны относительно β ; отсюда K'L' || P'Q' , K'P'|| L'Q' , т.е. плоский четырехугольник K'L'Q'P' – параллелограмм. Обозначим через O точку пересечения его диагоналей. Тогда MO – медиана, а значит, и биссектриса в равнобедренных треугольниках K'MQ' и L'MP' , что и требовалось доказать.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь