Назад

Олимпиадная задача по планиметрии для 10 класса: пересечение прямых в треугольнике ABC

Задача 210781 • Сложность: 4 • 10 класс
Задача

Прямые, содержащие медианы треугольника ABC, вторично пересекают его описанную окружность в точках A1, B1, C1. Прямые, проходящие через A, B, C и параллельные противоположным сторонам, пересекают ее же в точках A2, B2, C2. Докажите, что прямые A1A2, B1B2, C1C2 пересекаются в одной точке.

Авторы:
Заславский А. А. Илюхина М.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Олимпиада по геометрии имени И.Ф. Шарыгина II Олимпиада по геометрии имени И.Ф. Шарыгина (2006 г.)
Количество версий:
5
Решение
Автор: Илюхина М.
  Пусть A' – точка пересечения касательных к описанной окружности Ω в точках B и C (аналогично построим точки B' и C'). Тогда, как известно, прямая AA' является симедианой треугольника ABC (см. задачу 156983). Пусть прямая AA' вторично пересекает Ω в точке A0. Тогда  ∠A1AB = ∠A0AC, то есть дуги BA1 и CA0 равны. Так как треугольник A'BC равнобедренный, то эти дуги симметричны относительно биссектрисы l угла BA'C. Значит, при этой симметрии точки A1 и A0 переходят друг в друга.

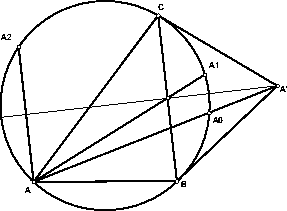
  Поскольку l – серединный перпендикуляр к BC, то A при этой симметрии переходит в A2 (см. рис.), а, следовательно, прямая A1A2 переходит в прямую AA'. Поэтому, так как прямые AA', BB', CC' пересекаются в одной точке L (см. задачу 156924), то прямые A1A2, B1B2, C1C2 также пересекаются в точке, изогонально сопряженной L относительно треугольника A'B'C'.

  Случай, когда одной из точек A', B', C' не существует, аналогичен.

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет