Олимпиадная задача по геометрии: пересечение прямых через точки A₁, B₁
Задача
На сторонах BC,CAи ABтреугольника ABCвзяты точки A1,B1и C1, причем прямые AA1,BB1и CC1пересекаются в одной точке P. Докажите, что прямые AA2,BB2и CC2, симметричные этим прямым относительно соответствующих биссектрис, тоже пересекаются в одной точке Q.
Решение
Можно считать, что точки A2,B2и C2лежат на сторонах треугольника ABC. Согласно задаче 5.78
$\displaystyle {\frac{AC_2}{C_2B}}$ . $\displaystyle {\frac{BA_2}{A_2C}}$ . $\displaystyle {\frac{CB_2}{B_2A}}$ = $\displaystyle {\frac{\sin ACC_2}{\sin C_2CB}}$ . $\displaystyle {\frac{\sin BAA_2}{\sin A_2AC}}$ . $\displaystyle {\frac{\sin CBB_2}{\sin B_2BA}}$.
Так как прямые AA2,BB2и CC2симметричны прямым AA1,BB1и CC1относительно биссектрис, то $\angle$ACC2=$\angle$C1CB,$\angle$C2CB=$\angle$ACC1и т. д., поэтому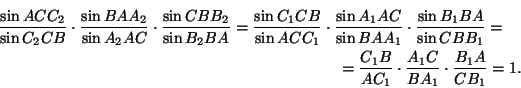
Следовательно,${\frac{AC_2}{C_2B}}$ . ${\frac{BA_2}{A_2C}}$ . ${\frac{CB_2}{B_2A}}$=1, т. е. прямые AA2,BB2и CC2пересекаются в одной точке. Замечание. Утверждение остается верным и в том случае, когда точки A1,B1и C1взяты на продолжениях сторон, если только точка Pне лежит на описанной окружности Sтреугольника ABC; если же Pлежит на окружности S, то прямые AA2,BB2и CC2параллельны (см. задачу 2.90).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет