Олимпиадная задача Горбачева: усложнения чисел и невозможность получить полный квадрат

Докажем, что среди 500-значных чисел найдётся искомое. Если 500-значное число усложнить 100 раз, получится 600-значное число. Существует менее 7·10²⁹⁹  600-значных полных квадратов  ((3·10²⁹⁹)² < 10⁵⁹⁹).  Зафиксируем k – один из этих квадратов. Количество чисел, из которых его можно получить описанной в условии операцией, не превосходит количества способов зачеркнуть в нем 100 цифр, то есть 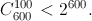   Таким образом, общее количество 500-значных чисел, из которых может быть получен полный квадрат, не превосходит  7·10²⁹⁹·2⁶⁰⁰ < 7·10²⁹⁹·8²⁰⁰ < 9·10⁴⁴⁹,  то есть меньше количества 500-значных чисел.

Существует.