Олимпиадная задача по планиметрии: доказательство углов в треугольнике для 8–11 классов
Задача
В треугольнике ABC AB – BC =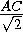 
. Пусть M – середина стороны AC, а BN – биссектриса. Докажите, что ∠BMC + ∠BNC = 90°.
Решение
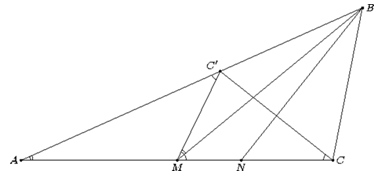
Пусть C' – точка, симметричная C относительно BN. Тогда AC' = AB – BC, и по условию AM : AC' = AC' : AC. Значит, треугольники AC'M и ACC' подобны, и ∠AC'M = ∠C'CA = 90° – ∠BNC (см. рис.). Применяя формулу для длины медианы (см. задачу 157592 а), получаем, что BM2 = AB·BC, то есть BC' : BM = BM : BA. Поэтому треугольники BC'M и BMA также подобны, и ∠BMC' = ∠BAM. Следовательно,
∠BMC = 180° – ∠BAM – ∠C'MA = ∠AC'M = 90° – ∠BNC.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет