Олимпиадная задача по планиметрии: центр вневписанной окружности в равнобедренном треугольнике
Задача
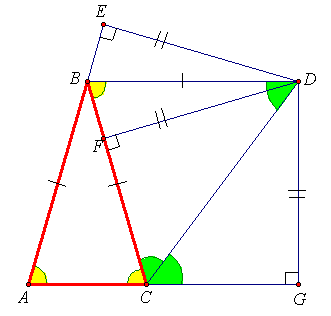
Дан равнобедренный треугольник ABC с основанием AC. Доказать, что конец D отрезка BD, выходящего из вершины B, параллельного основанию и равного боковой стороне треугольника, является центром вневписанной окружности треугольника.
Решение
BD – биссектриса внешнего угла B (см. задачу 153446). Треугольник CBD – равнобедренный, поэтому ∠GCD = ∠BDC = ∠DCB (G – точка на продолжении отрезка AC за точку C), то есть CD – биссектриса внешнего угла C. Точка D пересечения этих биссектрис, как известно, является центром вневписанной окружности.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет