Олимпиадная задача от Богданова И. И. на многочлены и делимость для 8-10 классов

Решение 1:   Для функции h(x) обозначим Δh(x) = h(x + 1) – h(x).   Лемма. Если Δh(x) в целых точках совпадает с многочленом степени не более  m – 1,  то h(x) в целых точках совпадает с многочленом степени не более m.

  Доказательство. Индукция по m. База:  m = 1.  Если Δh(x) равно константе c в целых точках, то  h(x) = h(0) + cx  при всех целых x.

  Шаг индукции. Пусть Δh(x) в целых точках совпадает с многочленом степени не более m и коэффициентом при x^m, равным a (возможно, нулевым). Обозначим  h₀(x) = h(x) – ¹/_(m+1) ax(x – 1)(x – 2)...(x – m + 1)(x – m).  Заметим, что  Δh₀(x) = Δh(x) – ax(x – 1)(x – 2)...(x – m + 1)  равно многочлену степени не более  m – 1  в целых точках. Следовательно, по предположению индукции, h₀(x) в целых точках совпадает с многочленом степени не более m. Так как  h(x) – h₀(x)  – многочлен степени не более  m + 1,  то и h(x) в целых точках совпадает с многочленом степени не более  m + 1.    Докажем теперь индукцией по k, что если в условиях задачи для каждого p многочлен Q_p(x) имеет степень, не большую k, то f(x) в целых точках совпадает с некоторым многочленом, степень которого тоже не больше k.

 База:  k = 0.  В этом случае нам известно, что для каждого простого p существует такая константа Q_p, что  f(x) – Q_p  делится на p при любом целом x. Но тогда  (f(x) – Q_p) – (f(0) – Q_p) = f(x) – f(0)  делится на p при любом целом x и любом простом p. Такое может быть, только если

f(x) = f(0),  то есть f(x) постоянна на целых числах.

  Шаг индукции. Функция Δf(x) удовлетворяет условию предположения индукции, так как  Δf(x) – ΔQ_p(x)  делится на p при любом целом x,

а ΔQ_p(x) – многочлен степени не выше  k – 1  (см. задачу 161433). Следовательно, Δf(x) совпадает в целых точках с многочленом степени не выше  k – 1.  По лемме f(x) совпадает в целых точках с многочленом степени не выше k.

Решение 2:   Выпишем интерполяционный многочлен Лагранжа, который совпадает с f(x) в точках 1, 2, ..., 2014 (см. задачу 161051):

  Положим  c= (2013!)².  Тогда коэффициенты многочлена cf₀(x) – целые числа. Пустьp– простое число, большееc. Многочлен  cQ_p(x) –cf₀(x)  имеет степень не выше 2013 и 2014 различных корней по модулюp– это числа 1, 2, ..., 2014 (поскольку  cQ_p(i) –cf₀(i) =c(Q_p(x) –f₀(i))  при  1 ≤i≤ 2014).  Поэтому этот многочлен тождественно равен нулю по модулюp. Значит, при любом целомxчисло  c(f(x) –Q_p(x)) +c(Q_p(x) –f₀(x)) =cf(x) –cf₀(x)  делится на любое достаточно большое простоеp. Следовательно,  f(x) =f₀(x)  при всех целыхx.

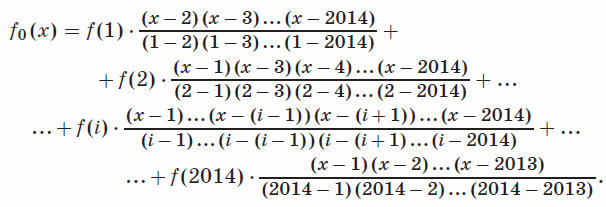
Ответ задачи отсутствует