Олимпиадная задача по планиметрии для 10-11 классов от Заславского А. А. — доказательство условии однопрямолинейности точек
Задача
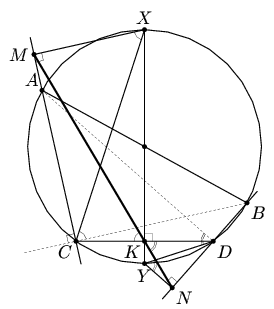
Hа окружности с диаметром AB выбраны точки C и D. XY – диаметр, проходящий через середину K хорды CD. Tочка M – проекция точки X на прямую AC, а точка N – проекция точки Y на прямую BD. Докажите, что точки M, N и K лежат на одной прямой.
Решение
Tак как ∠XKC = ∠XMC = 90°, то точки X, K, C и M лежат на одной окружности и ∠MKC = ∠MXC (см. рис.). Tак как XM || BC, то ∠MXC = ∠BCX. Аналогично ∠NKD = ∠ADY. Из равенства дуг AY и BX (на них опираются равные центральные углы) следует, что ∠NKD = ∠ADY = ∠BCX = ∠MKC, что и требовалось.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет