Олимпиадная задача по планиметрии: равнобедренные треугольники в четырёхугольнике (8-9 класс)
Задача
Дан выпуклый четырёхугольник. Если провести в нём любую диагональ, он разделится на два равнобедренных треугольника. А если провести в нём обе диагонали сразу, он разделится на четыре равнобедренных треугольника. Обязательно ли этот четырёхугольник – квадрат?
Решение
Всем условиям удовлетворяет равнобедренная трапеция с меньшим основанием, равным боковой стороне, и углами в 72° при большем основании.
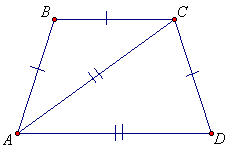
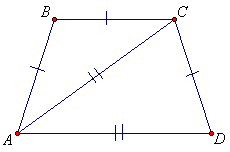
Ответ
Не обязательно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет