Олимпиадная задача про муравьев на доске 7×7: маршруты и пересечения, 8–9 класс
Задача
Два муравья проползли каждый по своему замкнутому маршруту на доске 7×7. Каждый полз только по сторонам клеток доски и побывал в каждой из 64 вершин клеток ровно один раз. Каково наименьшее возможное число таких сторон, по которым проползали и первый, и второй муравьи?
Решение
Пример, где число "общих" сторон равно 16, приведён на рисунке (один маршрут чёрный, другой – красный).
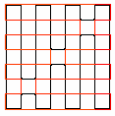
64 + 64 – 112 = 16.
Ответ
16 сторон.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет