Назад

Олимпиадная задача по планиметрии: центры окружностей треугольников на одной окружности (9-10 класс)

Задача 216556 • Сложность: 2 • 9-10 класс
Задача

На стороне AC остроугольного треугольника ABC выбраны точки M и K так, что ∠ABM = ∠CBK.

Докажите, что центры описанных окружностей треугольников ABM, ABK, CBM и CBK лежат на одной окружности.

Авторы:
Емельянова Т.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Всероссийская олимпиада по математике 2010-2011 Региональный этап
Количество версий:
5
Решение

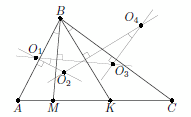
  Без ограничения общности можно считать, что точка M лежит между A и K. Пусть O1, O2, O3 и O4 – центры описанных окружностей треугольников ABM, ABK, CBM и CBK соответственно. Прямые O1O3 и O1O2 являются соответственно серединными перпендикулярами к отрезкам BM и AB. Значит, углы O2O1O3 и ABM равны как углы с взаимно перпендикулярными сторонами.

  Аналогично  ∠O2O4O3= ∠CBK,  а значит,  ∠O2O4O3= ∠O2O1O3.  Это и означает, что точкиO1,O2,O3,O4лежат на одной окружности.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет