Олимпиадная задача по планиметрии для 10-11 классов: медианы и окружности
Задача
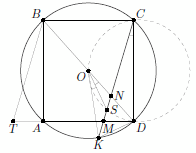
На окружности, описанной около прямоугольника ABCD, выбрана точка K. Оказалось, что прямая CK пересекает отрезок AD в такой точке M, что
AM : MD = 2. Пусть O – центр прямоугольника. Докажите, что точка пересечения медиан треугольника OKD лежит на описанной окружности треугольника COD.
Решение
Отметим на продолжении отрезка AD такую точку T, что AT = DM. Тогда BCMT – параллелограмм. Поскольку DT = DA + AT = 3DM + DM = 4DM, то по теореме Фалеса прямая CM пересекает отрезок BD в такой точке N, что DB = 4DN. Значит, DN = NO, то есть KN – медиана треугольника OKD.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет