Олимпиадная задача по математике 11 класс: складывание квадратной скатерти, Косухин
Задача
После обеда на прозрачной квадратной скатерти остались тёмные пятна общей площади S. Оказалось, что если сложить скатерть пополам вдоль любой из двух линий, соединяющих середины противоположных её сторон, или же вдоль одной из двух её диагоналей, то общая видимая площадь пятен будет равна S1. Если же сложить скатерть пополам вдоль другой её диагонали, то общая видимая площадь пятен останется равна S. Какое наименьшее значение может принимать величина S1 : S?
Решение
Назовём точки, покрытые пятнами, грязными. Для каждой точки P скатерти обозначим через f(P), g(P) и h(P) соответственно точки, симметричные ей относительно двух средних линий и первой диагонали скатерти, а через k(P) точку, симметричную точке P относительно второй диагонали. Заметим, что для любой точки P точки k(P) и h(f(g(P))) совпадают.
Предположим, что S1 < 2S/3. Тогда площадь множества всех грязных точек Q, для которых точка g(Q) тоже грязная, равна
2(S – S1) > 2S/3. Аналогично площадь множества всех грязных точек Q, для которых f(Q) – грязная, больше 2S/3.
Заметим, что если две фигуры имеют площади s1 и s2, а их объединение имеет площадь не больше S, то площадь их пересечения будет не меньше
s1 + s2 – S.
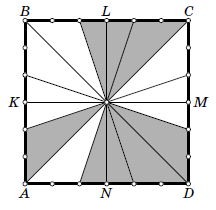
Поэтому площадь множества тех точек Q, для которых одновременно выполнены оба условия, больше 2S/3 + 2S/3 – S = S/3. Тем более, площадь множества всех грязных точек P, для которых f(g(P)) – грязная, больше S/3. Аналогично, площадь множества всех грязных точекR, для которыхg(f(R)) иh(R) грязны, больше S/3+2S/3–S= 0. Значит, и площадь множества грязных точекP, для которых точкаh(f(g(P))) – грязная, больше нуля. С другой стороны, h(f(g(P))) =k(P), а из условия следует, что площадь множества тех грязных точекP, для которыхk(P) – грязная, равна 0. Противоречие. Пример расположения пятен на скатерти, при котором S1:S= 2 : 3, показан на рисунке. Стороны "единичной" квадратной скатерти разделены отмеченными на ней точками на шесть равных частей. Здесь S= ½, S1= ⅓;.
Ответ
⅔.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь