Олимпиадная задача по математике: 100 точек в круге, планиметрия, 10

Задача

Внутри круга отмечены 100 точек, никакие три из которых не лежат на одной прямой.

Докажите, что их можно разбить на пары и провести прямую через каждую пару так, чтобы все точки пересечения прямых были в круге.

Решение

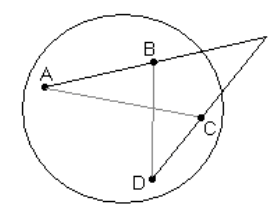
Разобьём точки на пары так, чтобы сумма длин соответствующих отрезков была максимальной. Допустим, для пар точек (A, B) и (C, D) прямые AB и CD пересекаются вне круга (см. рис.).

Тогда четырёхугольникABCD– выпуклый, AC + BD > AB + CD (см. задачу155152), то есть, разбив на пары по-другому, мы получили бы большую сумму длин отрезков. Противоречие.

Ответ

Ответ задачи отсутствует

Олимпиадная задача по планиметрии: пары точек и прямые в круге, Шаповалов, 10–11 класс

Задача

Решение

Ответ

Подтверждение удаления