Олимпиадная задача: может ли a + b + c + d быть простым, если ab = cd? Фольклор, 7–9 класс

  Первый способ.  a + b + c + d = a + b + c + = = = .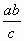

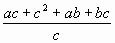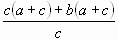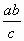  Полученное число – натуральное, при этом  а + с > c  и  b + c > c.  Следовательно, при сокращении дроби получится произведение двух множителей, отличных от 1, то есть составное число.   Второй способ. Согласно задаче 198256 найдутся такие натуральные u, v, w, z, что  a = uv,  b = wz,  c = uw,  d = vz.  Тогда

a + b + c + d = uv + wz + uw + vz = (u + z)(v + w).  Оба множителя больше единицы, значит, число  a + b + c + d  – составное.

Не может.