Олимпиадная задача по планиметрии: геометрическое место точек в квадрате (Френкин Б. Р.)
Задача
Дан квадрат. Найдите геометрическое место середин гипотенуз прямоугольных треугольников, вершины которых лежат на попарно различных сторонах квадрата и не совпадают с его вершинами.
Решение
Ясно, что середина гипотенузы лежит внутри квадрата. Если концы гипотенузы лежат на противоположных сторонах квадрата, то её середина лежит на соответствующей средней линии. Пусть теперь концы X и Y гипотенузы треугольника XYZ принадлежат соответственно сторонам AB и AD квадрата ABCD, а вершина Z – стороне BC (см. рис.). Обозначим через O середину XY. Точки A и Z лежат на окружности с диаметром XY; поэтому
OA = OX = OY = OZ, и расстояние от O до A меньше, чем до других вершин квадрата, но не меньше, чем расстояние от O до прямой BC.
Геометрическим местом точек, равноудаленных от A и BC, является парабола с фокусом A и директрисой BC (вершиной этой параболы является середина AB). Значит, точка O лежит между BC и этой параболой в четверти квадрата, содержащей A. При этом точка O может попасть на параболу, но не может – на среднюю линию (иначе точка Y совпадёт с B).
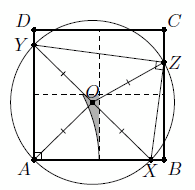
Ответ
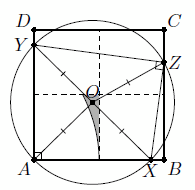
Все точки криволинейного восьмиугольника, ограниченного дугами восьми парабол с фокусами в вершинах квадрата и директрисами, содержащими несмежную сторону, кроме середин сторон квадрата (см. рис.).
Чтобы оставлять комментарии, войдите или зарегистрируйтесь