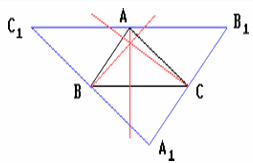
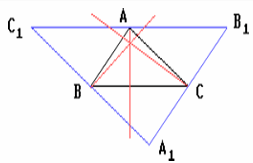
Первый способ. а) Проведём через вершины треугольника ABC прямые, параллельные его противоположным сторонам. В результате получим треугольник A₁B₁C₁, серединами сторон которого являются точки A, B и C. Высоты треугольника ABC являются серединными перпендикулярами к сторонам треугольника A₁B₁C₁, поэтому центр описанной окружности треугольника A₁B₁C₁ является точкой пересечения высот треугольника ABC.

 Второй способ. Если треугольник остроугольный, то его высоты лежат на биссектрисахортотреугольника(см. задачу152866) и поэтому пересекаются в одной точке.   Если же треугольник тупоугольный, то аналогично доказывается, что одна его высота лежит на биссектрисе одного из углов ортотреугольника, а две другие – на биссектрисах внешних углов ортотреугольника.   Для прямоугольного треугольника утверждение очевидно. б) Точка  H является центром описанной окружности треугольника A₁B₁C₁, поэтому   4R² = B₁H² = B₁A² + AH² = BC² + AH².  Следовательно,

Ответ задачи отсутствует