Задача
На сторонах треугольника ABC внешним образом построены квадраты с центрами A1, B1 и C1. Пусть a1, b1 и c1 – длины сторон треугольника A1B1C1, S и S1 – площади треугольников ABC и A1B1C1. Докажите, что:
а)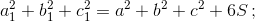 
б) S1 – S = 1/8 (a² + b² + c²).
Решение
а) По теореме косинусов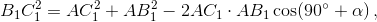 
то есть 
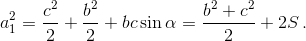Записывая аналогичные равенства для 
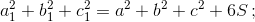и складывая их, получаем требуемое. б) Для остроугольного треугольника ABC, прибавив к S площади треугольников ABC1, AB1C и A1BC и прибавив к S1 площади
треугольников AB1C1, A1BC1 и A1B1C, получим одинаковые величины (для треугольника с тупым углом A площадь треугольника AB1C1 следует взять со знаком минус). Поэтому
S1 = S + ¼ (a² + b² + c²) – ¼ (ab cos γ + ac cos β + bc cos α). Остаётся заметить, что
ab cos γ + ac cos β + bc cos α = 2S(ctg γ + ctg α + ctg β) = ½ (a² + b² + c²) (см. задачу 157627, а).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь