Задача
Окружность радиуса ua вписана в угол A треугольника ABC, окружность радиуса ub вписана в угол B; эти окружности касаются друг друга внешним образом. Докажите, что радиус
описанной окружности треугольника со сторонами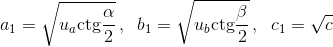 
равен 
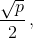где p – полупериметр треугольника ABC.
Решение
Длина общей касательной к данным окружностям равна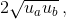 
поэтому
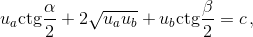то есть 
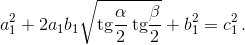Согласно задаче 157619 б)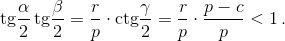 
Поэтому существует угол γ1, для которого
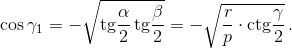
Мы проверили, что треугольник со сторонами a1, b1, c1 действительно существует; кроме того, угол между сторонами a1 и b1 равен γ1. Диаметр описанной окружности этого треугольника равен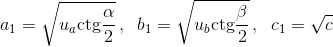 
поскольку
c = p – r ctg γ/2.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет