Задача
Окружность S1 вписана в угол A треугольника ABC. Из вершины C к ней проведена касательная (отличная от CA), и в образовавшийся треугольник с вершиной B вписана окружность S2. Из вершины A к S2 проведена касательная, и в образовавшийся треугольник с вершиной C вписана окружность S3
и т. д. Докажите, что окружность S7 совпадает с S1.
Решение
Пусть ri – радиус окружности Si, hi – высота треугольника ABC,
опущенная из вершины A при i = 3k + 1, из вершины B при i = 3k + 2, из вершины
C при i = 3k. Формулу из задачи 156838 а) можно записать в виде
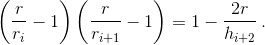
Перемножим i-е и (i+2)-е равенства, а затем поделив на (i+1)-е, получим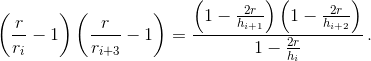 
Правая часть полученного выражения не изменяется при замене i на i + 3. Поэтому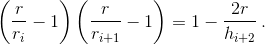 
Поскольку все треугольники невырожденные, r ≠ ri+3. Поэтому ri = ri+6.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь