Задача
В треугольнике ABC проведена биссектриса AD. Пусть O, O1 и O2 – центры описанных окружностей треугольников ABC, ABD и ACD.
Докажите, что OO1 = OO2.
Решение
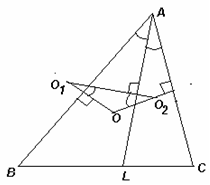
Проведём серединные перпендикуляры к отрезкам АВ, АС и AL, тогда вершинами треугольника ОO1O2 являются точки их попарного пересечения (см. рис.).
∠ОO1O2 = ∠BAL как острые углы с соответственно перпендикулярными сторонами. Аналогично ∠ОO2O1 = ∠СAL = ∠BAL = ∠ОO1O2, значит,
ОO1 = ОO2.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет