Олимпиадная задача: углы треугольника и центр описанной окружности
Задача
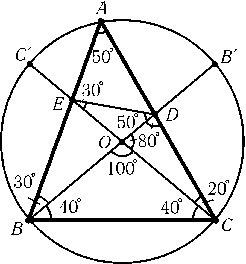
В остроугольном треугольнике ABCотрезки BOи CO, где O — центр описанной окружности, продолжены до пересечения в точках Dи Eсо сторонами ACи AB. Оказалось, что $\angle$BDE= 50oи $\angle$CED= 30o. Найдите величины углов треугольника ABC.
Решение
Поскольку $\angle$BDE= 50oи $\angle$CED= 30o, то $\angle$BOC=$\angle$EOD= 180o- 50o- 30o= 100o. Будем считать, что фиксированы диаметры BB'и CC'окружности, причем $\angle$BOC= 100o, а точка Aдвижется по дуге B'C'. Пусть D — точка пересечения BB'и AC, E — точка пересечения CC'и AB(рис. 12.6). Так как при движении точки Aот B'к C'отрезок OEувеличивается, а ODуменьшается, то угол OEDубывает, а угол ODEвозрастает. Поэтому существует единственное положение точки A, при котором $\angle$CED=$\angle$OED= 30oи $\angle$BDE=$\angle$ODE= 50o. Докажем теперь, что треугольник ABCс углами $\angle$A= 50o,$\angle$B= 70o,$\angle$C= 60oобладает требуемым свойством. Пусть A1...A18 — правильный восемнадцатиугольник. В качестве треугольника ABCможно взять треугольник A2A14A9. Диагональ A1A12проходит через точку E(см. решение задачи 12.58). Пусть F -- точка пересечения прямых A1A12и A5A14; прямая A9A16симметрична прямой A1A12относительно прямой A5A14, поэтому она проходит через точку F. В треугольнике CDFлуч CEявляется биссектрисой угла C, а прямая FE — биссектрисой внешнего угла при вершине F. Поэтому DE — биссектриса угла ADB, т. е. $\angle$ODE= ($\smile$A2A14+$\smile$A5A9)/4 = 50o.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь