Задача
Докажите, что касательная к вписанной окружности в точке(x0:y0:z0) задается уравнением
$\displaystyle {\frac{x}{\sqrt{x_0}}}$cos$\displaystyle {\frac{\alpha }{2}}$ + $\displaystyle {\frac{y}{\sqrt{y_0}}}$cos$\displaystyle {\frac{\beta }{2}}$ + $\displaystyle {\frac{z}{\sqrt{z_0}}}$cos$\displaystyle {\frac{\gamma }{2}}$ = 0.
Решение
Пусть точки(x0:y0:z0) и(x1:y1:z1) лежат на вписанной окружности. Тогда прямая, проходящая через эти точки, задается уравнением
x($\displaystyle \sqrt{y_0z_1}$ + $\displaystyle \sqrt{y_1z_0}$)cos$\displaystyle {\frac{\alpha }{2}}$ + y($\displaystyle \sqrt{x_0z_1}$ + $\displaystyle \sqrt{x_1z_0}$)cos$\displaystyle {\frac{\beta }{2}}$ + z($\displaystyle \sqrt{x_0y_1}$ + $\displaystyle \sqrt{x_1y_0}$)cos$\displaystyle {\frac{\gamma }{2}}$ = 0.
Проверим, например, что точка(x0:y0:z0) лежит на этой прямой. Для этого
воспользуемся тождеством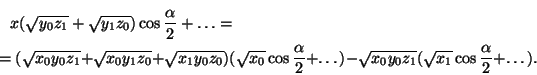
Точки(x0:y0:z0) и(x1:y1:z1) лежат на вписанной окружности, поэтому согласно задаче 14.42, б)$\sqrt{x_0}$cos${\frac{\alpha }{2}}$+...= 0 и$\sqrt{x_1}$cos${\frac{\alpha }{2}}$+...= 0. Чтобы получить уравнение касательной в точке(x0:y0:z0), нужно положитьx1=x0,y1=y0,z1=z0. После деления на2$\sqrt{x_0y_0z_0}$уравнение примет требуемый вид.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет