а) Описанная окружность задается уравнениемayz+bxz+cxy= 0, т. е.${\frac{a}{x}}$+${\frac{b}{y}}$+${\frac{c}{z}}$= 0 (здесьa,b,c — длины сторон треугольника). Одно доказательство этого утверждения содержится в решении задачи 5.10; другое -- в решении задачи 14.37. Еще одно доказательство можно получить, воспользовавшись тем, что описанная окружность изогонально сопряжена бесконечно удаленной прямой, которая задается уравнениемax+by+cz= 0. б) Вписанная окружность задается уравнениемcos${\frac{\alpha }{2}}$$\sqrt{x}$+ cos${\frac{\beta}{2}}$$\sqrt{y}$+ cos${\frac{\gamma}{2}}$$\sqrt{z}$= 0, т. е.

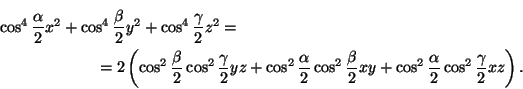
Чтобы получить это уравнение, можно воспользоваться тем, что вписанная окружность треугольникаABCявляется описанной окружностью треугольникаA₁B₁C₁, гдеA₁,B₁иC₁ — точки касания. Пусть(x₁:y₁:z₁) — трилинейные координаты точки описанной окружности треугольникаA₁B₁C₁. Тогдапоскольку углы треугольникаA₁B₁C₁равны${\frac{\beta+\gamma}{2}}$,${\frac{\alpha+\gamma}{2}}$,${\frac{\alpha+\beta}{2}}$. Согласно задаче2.58, б)xy=z₁². Кроме того,sin${\frac{\beta+\gamma}{2}}$= cos${\frac{\alpha }{2}}$. в) Вневписанная окружность, касающаяся стороныBC, задается уравнениемcos${\frac{\alpha }{2}}$$\sqrt{-x}$+ cos${\frac{\beta}{2}}$$\sqrt{y}$+ cos${\frac{\gamma}{2}}$$\sqrt{z}$= 0, т. е.
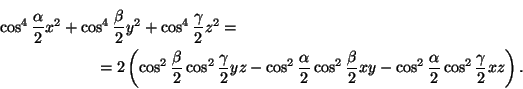
Это доказывается точно так же, как и для вписанной окружности.

Ответ задачи отсутствует