Задача
Докажите, что для любых натуральных m и n хотя бы одно из чисел 
, 
не больше 
.
Решение
Если n ≥ m, то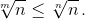 
Поэтому достаточно доказать, что 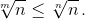то есть что 3n ≥ n3. Докажем это по индукции.
База: 31 > 1³, 3² > 2³, 3³ = 3³.
Шаг индукции. 3n+1 = 3·3n ≥ 3n³ > (n + 1)³, поскольку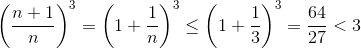 
при n ≥ 3.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет