Задача
Докажите, что если α < 0 < β, то
Sα(x) ≤ S0(x) ≤ Sβ(x), причём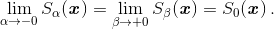 
Определение средних степенных Sα(x) можно посмотреть в справочнике.
Решение
Оба неравенства следуют из неравенства Иенсена (см. задачу 161407), применённого к функции f(x) = eαx и точкам ln x1, ..., ln xn.
Для подсчёта пределов воспользуемся приближённой формулой для функции ex, которая верна на отрезке x ∈ [–1, 1]: ex = 1 + x + θx² (|θ| < 1).
При достаточно малом α получим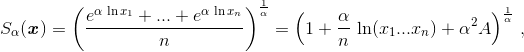 
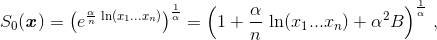где A = θ1n–2(ln²x1 + ... + ln²xn), B = θ2n–2 ln²(x1...xn), |θ1|, |θ2| < 1. Поэтому
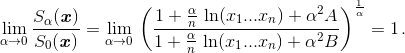
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет