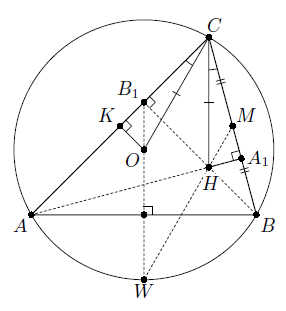
Пусть AA₁, BB₁ и CC₁ – высоты треугольника ABC, O – центр его описанной окружности.   Первый способ. Достаточно доказать два утверждения:

   1) прямая B₁O проходит через середину W дуги AB.

   2) прямые B₁O и HM симметричны относительны биссектрисы l_c угла C (см. рис. а).

  Первое утверждение следует из того, что  ∠A = 45°,  следовательно, треугольник ABB₁ – равнобедренный прямоугольный, то есть точки B₁ и O лежат на серединном перпендикуляре к отрезку AB.

  Для доказательства второго утверждения используем два факта:

   а) прямые CO и CH симметричны относительно биссектрисы l_c (см. задачу 152358).

   б) Если  ∠C = 60°,  то  CH = CO,  а CM = CB₁.

 Действительно пусть K – середина стороны AC. Тогда  CK = ½ AC = A₁K = CA₁,  и треугольники KCO и A₁CH равны по катету и прилежащему углу. Кроме того,  CM = ½ BC = CB₁.

  Второй способ. Пусть W – середина дуги AB. Тогда  ∠BOW = ½ ∠BOA = 60°,  следовательно, треугольник BOW – равносторонний (см. рис. б). Выше было доказано, что  CH = OC.  Значит,  CH = OW  и  CH || OW,  следовательно, OCHW – параллелограмм.

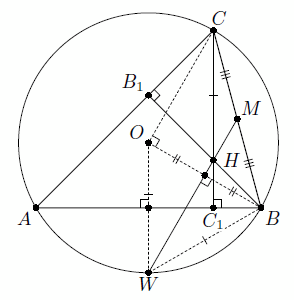
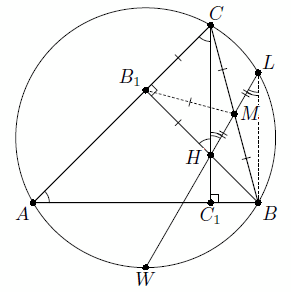
 ∠COB = 2∠CAB = 90°,  то есть  BO⊥WH.  Поэтому высота WH равнобедренного треугольника BWO делит отрезок BO пополам, а значит, содержит среднюю линию треугольника BOC, то есть проходит через точку M.   Третий способ. Пусть W – точка пересечения луча MH с описанной окружностью (см. рис. в).

  Поскольку B₁M – медиана прямоугольного треугольника с углом 60°, то  BM = CM = CB₁ = B₁M  и  ∠BB₁M = 30°.  Кроме того,

∠ACC₁ = 90° – ∠A = 45°.  Следовательно, прямоугольный треугольник HB₁C – равнобедренный.   Поэтому треугольник B₁HM – равнобедренный с углом 30° при вершине. Следовательно,  ∠CHM = ∠B₁HM – ∠B₁HC = 75° – 45° = 30°.

  Пусть точка L симметрична точке H относительно точки M. Тогда HBLC – параллелограмм, и  ∠HLB = ∠CHL = 30°.  Поскольку L лежит на описанной окружности (см. задачу 208949), то W – середина дуги AB.

Ответ задачи отсутствует