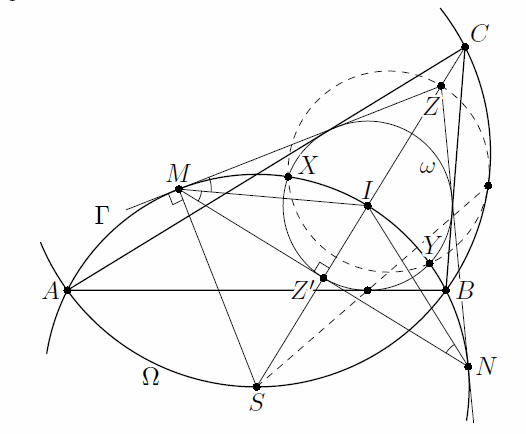
Пусть биссектриса CI повторно пересекает описанную окружность Ω треугольника ABC в точке S. Тогда точка S – центр окружности Г (см. задачу 153119). Из симметрии точка Z лежит на прямой SC.

  Пусть общие касательные к окружностям ω и Г касаются Г в точках M и N (см. рис.). Линия центров SI является серединным перпендикуляром к отрезку MN, а прямая MZ касается Г, то  ∠IMN = ∠INM = ∠IMZ.  Значит, MI – биссектриса угла ZMN, то есть расстояния от I до ZM и MN равны. Поскольку ω касается ZM, она также касается прямой MN в некоторой точке Z'; из симметрии, эта точка лежит на SI.

  Из прямоугольного треугольника SMZ получаем  SZ·SZ' = SM²  (см. задачу 156452). Это означает, что при инверсии относительно окружности Г точка Z' перейдёт в точку Z. Значит, окружность ω, содержащая точки X, Y и Z', перейдёт в описанную окружность треугольника XYZ. При этой инверсии прямая AB переходит в окружность Ω. Поскольку ω и AB касаются, их образы также будут касаться, что и требовалось.

Ответ задачи отсутствует