Задача
Отрезок AD – диаметр описанной окружности остроугольного треугольника ABC. Через точку H пересечения высот этого треугольника провели прямую, параллельную стороне BC, которая пересекает стороны AB и AC в точках E и F соответственно.
Докажите, что периметр треугольника DEF в два раза больше стороны BC.
Решение
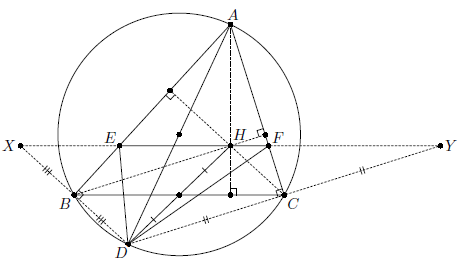
Пусть X и Y – точки пересечения прямых BD и CD с прямой EF (см. рис.). Как известно (см. задачу 208949), точки D и H симметричны относительно середины стороны BC. Отсюда следует, что BC – средняя линия треугольника XYD. Заметим, что углы ABD и ACD – прямые. Поэтому XE = DE,
YF = DF, и следовательно, DE + EF + DF = XE + EF + FY = XY = 2BC.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет