Задача
В остроугольном треугольнике ABC, в котором ∠A = 45°, проведены высоты AA1, BB1, CC1. Биссектриса угла BAA1 пересекает прямую B1A1 в точке D, а биссектриса угла CAA1 пересекает прямую C1A1 в точке E. Найдите угол между прямыми BD и CE.
Решение
Решение 1: Прямая A1A является биссектрисой угла B1A1C1 (см. задачу 152866). Кроме того, ∠ B1A1C = ∠C1A1B = ∠A (см. задачу 152357). Значит, ∠ B1A1C1 = 90°, а ∠AA1C = ∠AA1B1 = 45°.
Пусть K и L – точки пересечения прямой AA1 c прямыми CE и BD соответственно. Из вышесказанного следует, что ∠BA1D = ∠DA1L = 45°. Следовательно, A1D – биссектриса угла BA1L. Поэтому D – центр вневписанной окружности треугольника BAA1. Значит, BD – биссектриса внешнего угла B. Аналогично E – центр вневписанной окружности треугольника CAA1, а CE – биссектрисса внешнего угла C.
Пусть M – точка пересечения прямой CE с прямой BD, тогда ∠BMC = 180° – ½ (180° – ∠C) – ½ (180° – ∠B) = ½ (∠B + ∠C) = 67,5°.
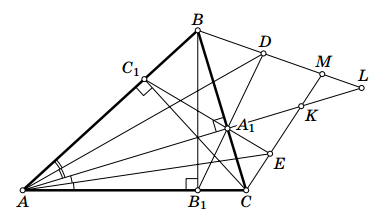
Решение 2: Пусть ∠BAA1 = 2β, ∠CAA1 = 2γ. Так как 2β + 2γ = 45°, то β + γ = 22,5°.
Точки A1 и B1 лежат на окружности с диаметром AB, поэтому ∠AA1B1 = ∠ABB1 = 45°.
Из треугольника ADA1 получаем ∠B1DA = 45° – β = 2(β + γ) – β = 2γ + β = ∠B1AD. Поэтому B1D = B1A = B1B. Пользуясь вписанными углами, находим ∠DB1B= ∠A1B1B= ∠A1AB= 2β. Так как треугольникBB1Dравнобедренный, то ∠B1BD= ½ (180° – 2β) = 90° – β. Кроме того, ∠A1BB1= ∠A1AB1= 2γ, значит, ∠A1BD= 90° – β – 2γ. Аналогично ∠A1CE= 90° – γ – 2β. Следовательно, искомый угол равен 180° – ∠A1BD– ∠A1CE= 3(β + γ) = 3·22,5° = 67,5°.
Ответ
67,5°.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь