Задание олимпиады: биссектрисы и окружности в трапеции
Задача
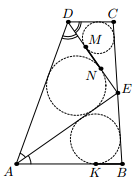
В трапеции ABCD биссектрисы углов A и D пересекаются в точке E, лежащей на боковой стороне BC. Эти биссектрисы разбивают трапецию на три треугольника, в которые вписали окружности. Одна из этих окружностей касается основания AB в точке K, а две другие касаются биссектрисы DE в точках M и N. Докажите, что BK = MN.
Решение
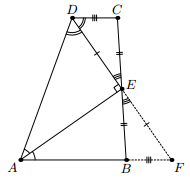
Заметим, что ∠AED = 90° (сумма углов A и D равна 180°, DE и AE – биссектрисы, см. рис. слева). Пусть F – точка пересечения прямых DE и AB. В треугольнике ADF отрезок AE является высотой и биссектрисой, следовательно, этот треугольник – равнобедренный и DE = EF. Поэтому треугольники DCE и FBE равны по стороне и двум углам. Следовательно, CE = BE и DC = FB, откуда AD – CD = AF – CD = AB.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь