Пересечение прямых в задаче с вневписанными окружностями
Задача
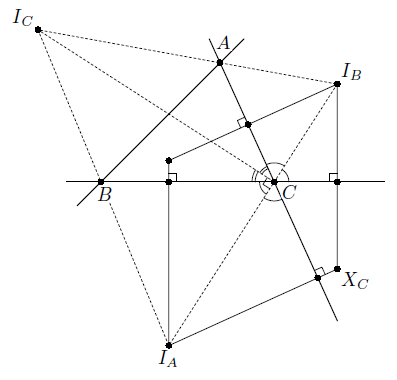
Точки IA, IB, IC – центры вневписанных окружностей треугольника ABC, касающихся сторон BC, AC и AB соответственно. Перпендикуляр, опущенный из IA на AC, пересекает перпендикуляр, опущенный из IB на BC, в точке XC. Аналогично определяются точки XA и XB. Докажите, что прямые IAXA, IBXB и ICXC пересекаются в одной точке.
Решение
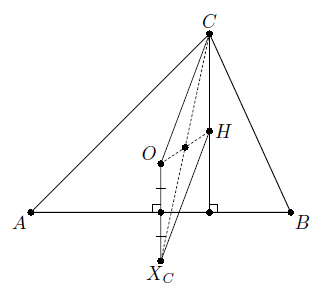
Так как центры вневписанных окружностей равноудалены от прямых, содержащих стороны треугольника, то прямая IAXC симметрична прямой, проходящей через IA и перпендикулярной BC, относительно прямой IAIB. Аналогично рассматривается симметрия прямой IBXC относительно прямой IAIB. Следовательно, точка XC симметрична точке пересечения перпендикуляров к сторонам BC и AC треугольника, проведённых из точек IA и IB соответственно, относительно прямой IAIB. Аналогично можно определить точки XA и XB.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь