Пусть IH – высота треугольника BIC. Докажем, что четырёхугольник C₁IB₁H – параллелограмм, откуда и будет следовать утверждение задачи.   Первый способ.  ∠AIC = 90° + ½ ∠B   (см. задачу 155448). Следовательно,  ∠B'IC = ½∠B.  Аналогично  ∠C'IB = ½ ∠C.  Значит, треугольники BIC, BC'I и IB'C – подобны (рис. слева).

  Поскольку IH и B'B₁ – соответствующие высоты в подобных треугольниках, то  BH : HC = IB₁ : CB₁,  откуда следует, что  HB₁ || BI.  Аналогично

HC₁ || CI,  то есть C₁IB₁H – параллелограмм.

  Второй способ. Пусть M и K – точки пересечения BC с прямыми C’C₁ и B’B₁ соответственно (рис. справа). Тогда треугольники C'BM и B'CK – равнобедренные, откуда C₁ и B₁ – середины отрезков C'M и B'K соответственно. Кроме того,  IM = IC' = IB' = IK.  Следовательно, треугольник MIK – равнобедренный, откуда  MH = HK.

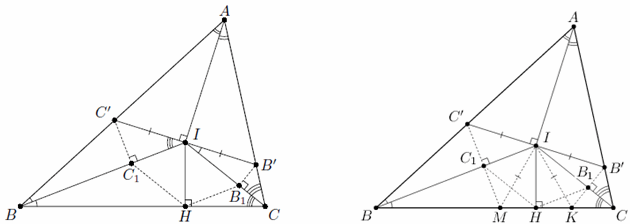
  Таким образом, точки I, C₁, H и B₁ являются серединами сторон четырёхугольника C'MKB', то есть образуют параллелограмм (см. задачу 153475).

Ответ задачи отсутствует